Linear regression(선형 회귀) 개념을 보기에 앞서, 먼저 용어를 살펴보겠습니다.
- Regression: 여러 독립 변수가 있을 때, 종속변수가 어떻게 변할 지 예측하는 모델(식)을 찾는 것을 말합니다.
- 독립 변수: 예측하고자 하는 값의 변화를 알기 위해 사용될 수 있는 값, 의도적으로 변화시킬 수 있는 값
- 종속 변수: 예측하고자 하는 값, 독립 변수에 의해 변하는 값
위의 용어를 생각해보면 Linear regression은 독립 변수(x)가 주어졌을 때 종속 변수(y)를 가장 잘 표현하는 선(Linear, 선을 표현하는 수학적 식)을 찾는 것이라 이해할 수 있습니다. 그리고 이러한 식을 찾기 위해서 우리는 미리 그 식의 틀을 아래와 같이 잡을 수 있습니다. 독립 변수 x가 여러 개(n개)가 있다면 다음과 같은 식으로 표현할 수 있겠지만,
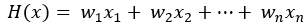
독립변수를 하나로 보고, 간단하게 선을 표현하는 다음 식을 생각해 보겠습니다.

이처럼 어떤 데이터가 분포할 것이라고 예상하는 위치를 표현하는 식(H(x))을 Hypothesis(가설)이라고 합니다.
Hypothesis는 위처럼 간단한 식이 될 수도 있고, 다음 포스팅에서 다룰 CNN이나 RNN으로 엮인 복잡한 식이 될수도 있습니다. 데이터가 어떤 특성, 분포를 갖고 있는지 어느 정도 알 수 있다면 Hypothesis 식을 세우는데 도움이 되고, 이러한 Hypothesis 식을 미리 세우는 것이 모델링의 시작이 됩니다. 선형적으로 분포한다는 사실을 그래프(평면) 상에서 먼저 알아낼 수 있었다면 위와 같이 Hypothesis를 세우고 W와 b 값을 찾아갈 수 있을 것입니다. 그리고 그 Hypothesis에 대한 parameter들 (여기서는 W, b)을 찾을 수 있다면, 주어진 input 데이터(x)로 실제 값(y)을 예측 할 수 있습니다.
아래와 같은 데이터를 가정해보겠습니다.
| x | y |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
이 데이터를 아래와 같이 평면 상에서 생각해본다면, 빨간 선이 이 데이터를 가장 잘 표현하고 있다는 것을 직관적으로 알 수 있고, 아래와 같은 식으로 정의할 수 있음을 알 수 있습니다. 하지만, 이러한 데이터(x, y)가 매우 많아서 어떤 선이 그 데이터를 가장 잘 표현하는 식인지 알려면 어떻게 할 수 있을까요?


여기에서 Cost function(비용 함수)라는 개념이 필요하게 됩니다. Cost function은 모든 input 데이터(x)에 대해 우리가 Hypothesis로 세운 식 간의 오차의 평균을 계산하는 함수입니다. Linear regression 에서 단순하게 생각했을 때 아래와 같이 Cost function을 정의할 수 있을 것입니다. (cost = 예측 값 - 실제 값)

하지만 이 경우, 예측 값과 실제 값의 차이 계산 시 음수가 발생하여, 실제로는 오차가 있지만 상쇄되어 작아질 수 있기 때문에 일반적으로 아래와 같이 차이의 제곱의 평균을 cost function으로 정의합니다 (MSE, Mean Square Error, 제곱 평균 오차). 그리고 MSE는 그 거리(오차)가 클 수록 penalty를 주는 효과가 있기 때문에 데이터를 잘 표현하는 정도를 더 효과적으로 나타낼 수 있습니다. 결론적으로, Linear regression 식을 찾기 위한 핵심 지표는 이 cost function을 최소화 하는 것이 되게 됩니다.

다음 포스팅에서는 이 cost function을 어떻게 작게 하고, 그에 따른 parameter (여기에서는 W, b)를 어떻게 찾을 수 있을지 다뤄보겠습니다.
참고한 자료1: https://hunkim.github.io/ml/
모두를 위한 머신러닝/딥러닝 강의
hunkim.github.io
참고한 자료2: https://drhongdatanote.tistory.com/14
[개념 통계 05] 독립변수와 종속변수는 무엇인가?
안녕하세요. 홍박사입니다. 오늘은 변수와 관련해 마지막 포스팅을 해보려고 합니다. 오늘 다룰 변수는 독립변수와 종속변수입니다. 사실상 독립변수와 종속변수는 중고등학교 과학 시간에도
drhongdatanote.tistory.com
참고한 자료3: https://john-analyst.medium.com/%ED%9A%8C%EA%B7%80-regression-%EB%9E%80-398c548e1560
회귀(regression)란.
통계학에서 회귀란, 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭한다.
john-analyst.medium.com
Loss Function, Cost Function, Objective Function의 차이
모델을 학습할 때는 비용(cost) 즉, 오류를 최소화하는 방향으로 진행이 된다. 비용이 최소화되는 곳이 성능이 가장 잘 나오는 부분이며, 가능한 비용이 적은 부분을 찾는 것이 최적화(Optimization)
bin-kkwon.tistory.com
'딥러닝 기초' 카테고리의 다른 글
| 5-1. Softmax (Multinomial classification) (0) | 2023.08.15 |
|---|---|
| 4-2. Logistic regression의 Cost function, Gradient descent (0) | 2023.08.15 |
| 4-1. Logistic regression (0) | 2023.08.13 |
| 3. 여러 개의 변수를 갖는 Linear regression (0) | 2023.08.06 |
| 2. Linear regression의 cost 함수를 최소화하는 방법 (0) | 2023.07.30 |



